Java continuously introduces new, useful features. For instance, Java 8 introduced the Stream API, one of the biggest highlights of the past few years. But is aggregating data with the Stream API a panacea? In this article, I’d like to explore if there’s a better alternative for certain cases from a complexity perspective.

Some of you have probably used the following code in a program in order to spontaneously measure a logic’s runtime:

long start = System.currentTimeMillis();
doSomething();
long time = System.currentTimeMillis() - start;

Clearly, it’s easy to implement and you can quickly check the code’s speed. But there are also some disadvantages. First, the measured values can contain uncertainties as they can be influenced by other processes running on the same machine. Second, you can’t compare the readings with other readings taken from different environments. Declaring that one solution is faster than the other isn’t helpful if they were measured on different machines with different CPUs and RAM. Third, it’s difficult to estimate how the runtime could extend when working with larger amounts of data in the future. It’s become much easier to filter and aggregate data since the Stream API was introduced in Java 8. The Stream API even opens up the possibility to parallelize processing [1]. But do these solutions continue to perform when you need to work with 10 or 100 times the amount of data? Is there a measurement that we can use to answer this question?

Time complexity

Time complexity is a measurement for roughly estimating the time efficiency of an algorithm. It focuses on how runtime increases as the input gets longer. For example, if you iterate a list of n elements with a for loop, then n and the runtime have a linear relationship. If you have multiple for loops nested and executed n times each, then this logic has an exponential effect on runtime.

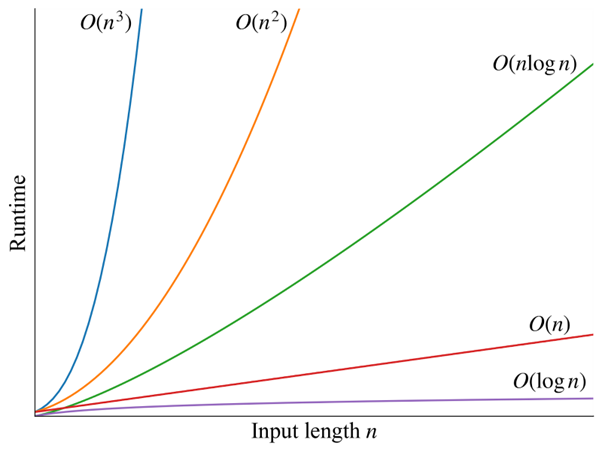
Big O notation is a way to represent the relationship between the input length and the runtime. A linear relationship is represented by O(n), O(n²) represents a quadratic relationship, where n is the input’s length. If the runtime is independent of the input’s length and is constant, then we write O(1). Figure 1 shows typical big O notation values for how the runtime grows as the input’s length increases.

Fig. 1: The relationship between runtime and input length per time complexity.

There are two important rules for representation using big O-notation:

Only the term with the highest degree is considered. For example: If the time complexity is n + nlogn + n², simply write O(n²), as the term n² has the strongest effect on runtime.
The coefficient is not considered. For example, the time complexity of 2n², 3n², and ½n² is equal to O(n²).

It’s important to emphasize that time complexity only focuses on scalability. Especially when n is a smaller value, one algorithm may have a longer runtime even if it has a better time complexity than others.

Space complexity

In addition to time complexity, there’s another measure for representing an algorithm’s efficiency: space complexity. It looks at how memory requirements grow as the input’s length increases. When you copy a list with n elements into a new list, the space complexity is O(n) because the need for additional memory increases linearly when you work with a larger input list. If an algorithm only needs a constant amount of memory, regardless of the input length, then the space complexity is O(1).

There’s often a trade-off relationship between time complexity and space complexity. Depending on the case, when comparing multiple algorithms, it’s important to consider if runtime or memory is more important.

Binary search

As shown in Figure 1, an algorithm with time complexity O(logn) has better time performance than O(n). Binary search is one of the algorithms with this time complexity. It’s applicable when you want to search for a target value from a sorted list. In each operation, the algorithm compares if the target value is in the left or right half of the search area. For example, imagine a dictionary. You probably won’t start on the first page of the dictionary to find the word you’re looking for. You’ll open up to a page in the middle of the book and start searching from there.

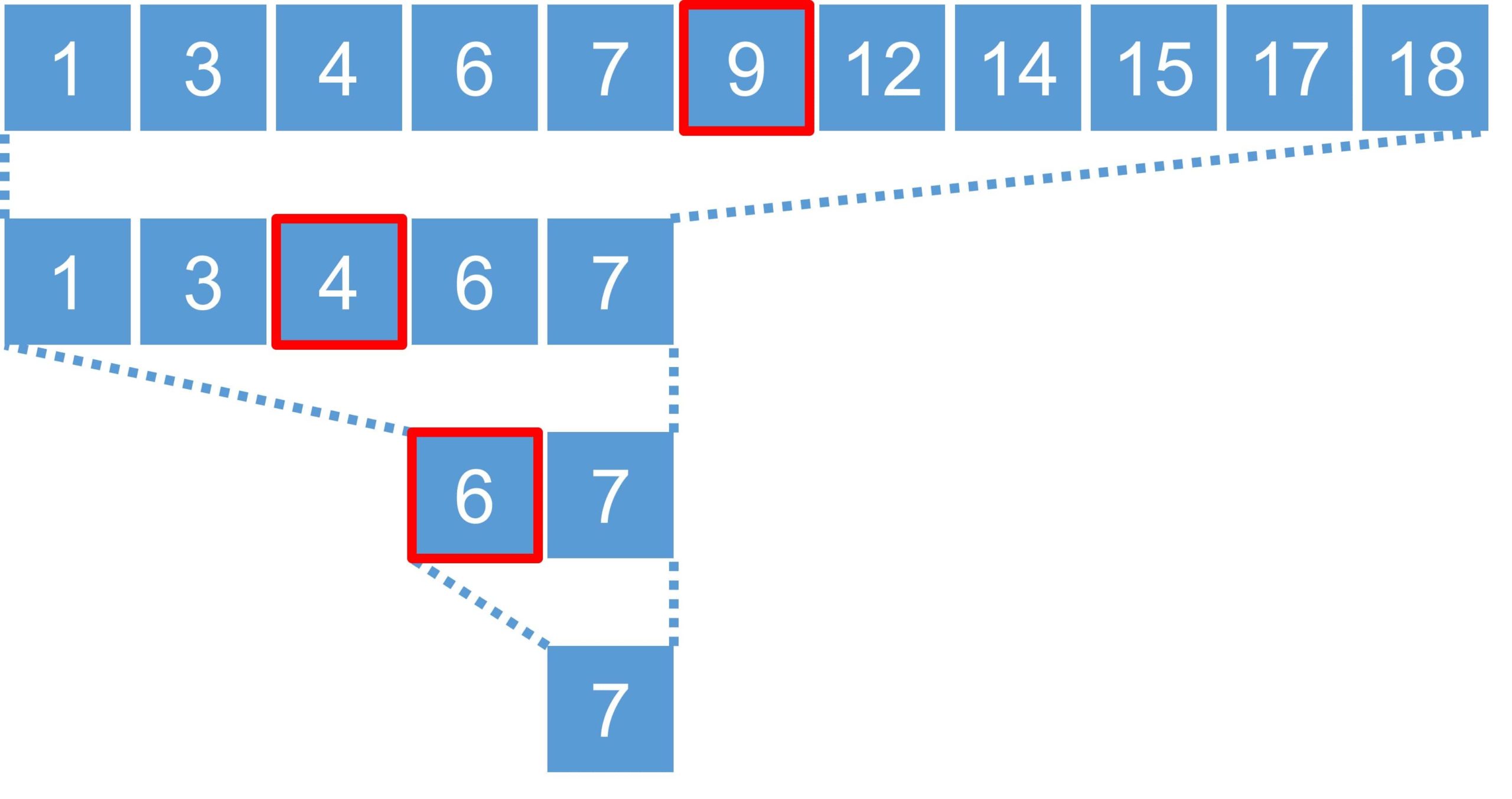
Fig. 2: Binary search sequence

Figure 2 shows how the binary search proceeds when searching for the target value 7 in a list of eleven elements. The element marked in red represents the middle of the current operation’s search area. If the number of elements in the search area is an even number, then it takes the “left” element in the middle. In each operation, you compare if the target value (7, in this case) is less than or greater than the middle. Cut the search area in half until you reach the target value.

log₂n is the maximum number of necessary comparison operations to find the target value with the binary search, where n is the length of the input list. Let’s take n = 8 as an example. The length of the search area starts with 8 and decreases to 4 after the first operation. After the second operation, it is divided in half again to 2 and after the third operation, there’s just one value in the search area. From this example, we can conclude that the number of operations needed is at most a logarithm of 8 to the base 2 (log₂8 = 3), because 2³= 8. In big O notation, we omit the base and write only O(logn).

In Java, implementation of binary search is found in the java.util.Arrays.binarySearch [2] and java.util.Collections.binarySearch methods [3]. If you work with an array, you can use the methods in the java.util.Arrays. If you work with a list, then the methods in the class java.util.Collections are applicable.

Sorting algorithm

There are several kinds of sorting algorithms, each with different time complexities and space complexities. In practice, typical sorting algorithms used are Quicksort, Mergesort, and their variants. On average, the time complexity of these two methods is O(nlogn) [4], [5]. There are also sorting algorithms with better time complexities, but these often have limitations in the arrangement of input list or require special hardware.

The methods for sorting in Java are implemented in java.util.Arrays.sort [2] and java.util.Collections.sort [3]. Since Java 8, the List interface also provides the sort method [6], while the Stream API has the intermediate sorted operation [1]. According to Java documentation, these methods are implemented by default with Quicksort, Timsort, or Mergesort. But this can vary depending on the JDK vendor.

Task 1: Searching in a sorted list

The first task is finding the target value in an already sorted list. One potential solution is using the contains method of the List interface (Listing 1).

Listing 1

// input
List<Integer> list = List.of(12, 15, 19, 20, 21, 24);
int target = 19;
// solution
boolean answer = list.contains(target);

This solution’s time complexity is O(n). In the worst case, it searches the whole list until you reach the end. Another solution is to take advantage of the fact that the input list is already sorted, so the binary search is applicable (Listing 2). Collections.binarySearch returns an integer greater than or equal to 0 if the target value is in the list. The two solutions’ space complexity is O(1) since they only need a consistent amount of memory to fix the result, regardless of input values.

Listing 2

// input
List<Integer> list = List.of(12, 15, 19, 20, 21, 24);
int target = 19;
// solution
boolean answer = Collections.binarySearch(list, target) >= 0;

I generated test data with 10³ and 10⁴ elements and used it to compare the runtime for the two solutions. The target values for the search are selected at regular intervals and the runtime was measured multiple times for each target value. The tests were run on a Windows 10 PC with Intel Core i7-1065G7 CPU 1.30GHz and 32 GB RAM. I used the Amazon Corretto 11.0.11 JDK and runtimes were measured with the Java Microbenchmark Harness [7].

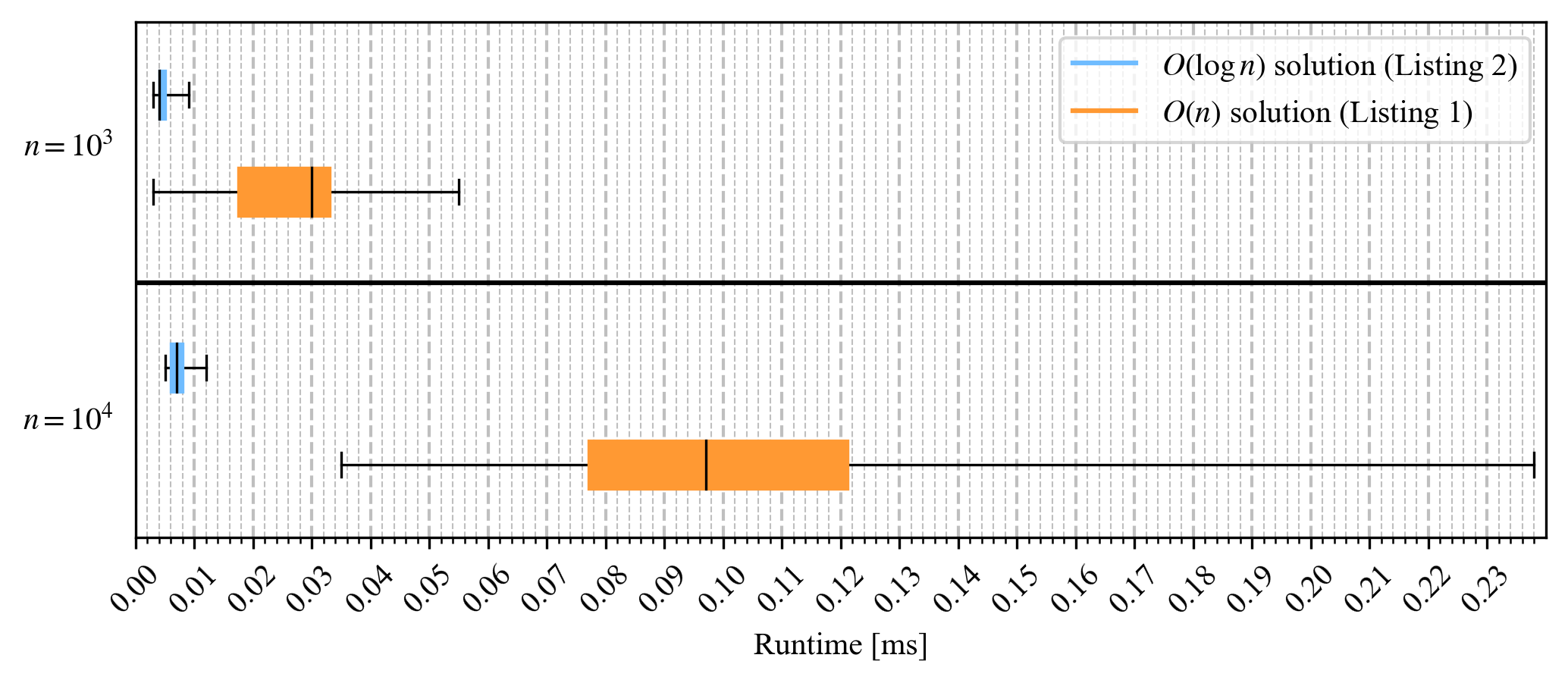
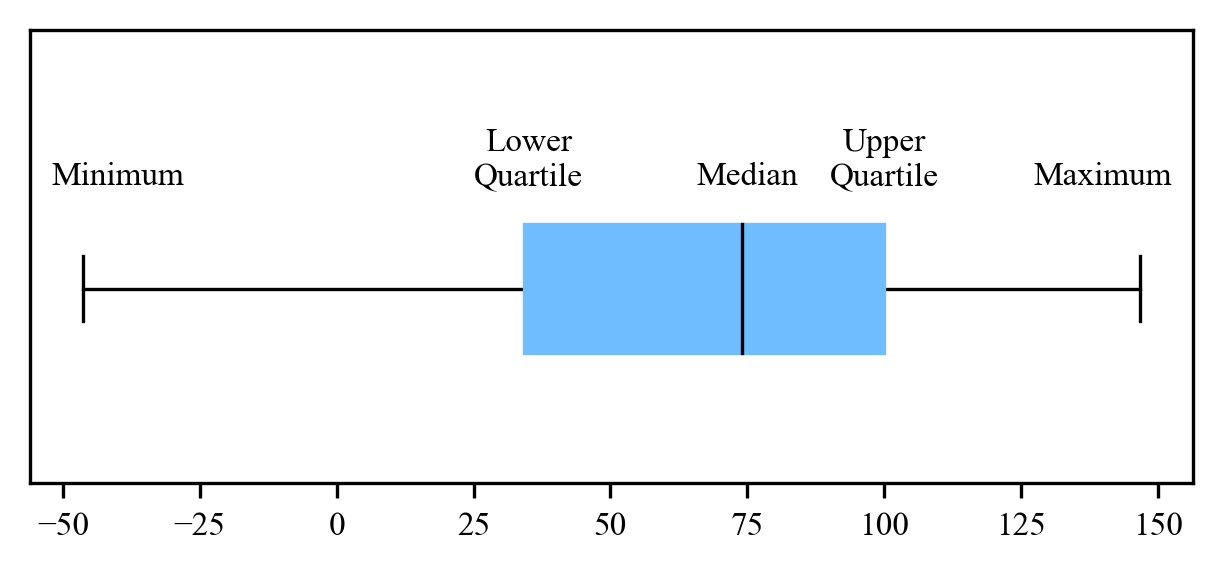
Figure 3 shows the results for each length of input as a box plot. Each box plot contains the measurements of calls that were executed with different target values. A box plot graphically represents the distribution of measurement results and represents the median, the two quartiles (whose intervals contain the middle 50% of the data), and the two minimum and maximum values of the data (Fig. 4). You can see in Figure 3 that the solution’s runtime in Listing 1 is more scattered than the binary search in Listing 2. This is because the runtime of the solution in Listing 1 heavily depends on where the target value is located in the list. This tendency becomes clearer when comparing results between the test cases n = 10³ and n = 10⁴. Between the two cases, the worst-case runtime of Listing 1 increased significantly compared to Listing 2.

Fig. 3: Running times of the respective solutions for task 1

Fig. 4: Box Plot

Task 2: Searching a range of values in a sorted list

The next task is counting the occurrence of values in a sorted list greater than or equal to a and less than b (a ≤ xi < b) where xi is the respective value in the input list. The requirements are that the input values a and b must always satisfy a ≤ b and there must not be any duplicates in the input list. An intuitive idea is using the intermediate operation filter in the Stream API to collect just the elements in a specific range of values, and ultimately, count the number of elements with the terminal operation count (Listing 3).

Listing 3

// input
List<Integer> list = List.of(12, 15, 19, 20, 21, 24);
int a = 14, b = 19;


// solution
long answer = list.stream().mapToInt(Integer::intValue)
.filter(value -> a <= value && value < b).count();

The time complexity of this solution is O(n), because you must iterate once through the whole list, checking each list element to see if the value is in the range. But is it possible to use binary search for this task too? What if we could set the following two pieces of information:

- - - Position of the value a in the input list, if included. Otherwise, the position in the input list where you can insert the value a.

- - - Position of the value b in the input list, if included. Otherwise, the position in the input list where you can insert the value b.

The difference between the two calculated positions is the number of elements between the two thresholds. In this solution, the binary search is performed twice. But since we don’t consider the coefficient in the big O notation, the time complexity of this solution is still O(logn). This is for the same reason as in Task 1: The space complexity of the two solutions is O(1). Listing 4 shows a sample implementation for this solution. Be aware that this code will not work if the input list has duplicates. As described in the documentation of Collections.binarySearch [3], the method does not guarantee which one will be found if the target value is included more than once in the list.

Listing 4

// input List<Integer> list = List.of(12, 15, 19, 20, 21, 24);
int a = 14, b = 19;

// solution
int lower = Collections.binarySearch(list, a);
int upper = Collections.binarySearch(list, b);
lower = lower < 0 ? ~lower : lower;
upper = upper < 0 ? ~upper : upper;
int answer = upper - lower;

Collections.binarySearch returns an integer greater than or equal to 0 if the target value is in the list. Otherwise, it returns a negative value where -(insertion point)-1 is. The insertion point is the position in the list where the target value should be inserted in order to keep the list sorted. In order to calculate the insertion point back from the return value -(insertion point)-1, you can simply use the bitwise NOT operator ~.

Just like with Task 1, Figure 5 plots the running times of the two solutions as a box plot, measured with different lengths of input and target values. Again, it’s easy to see that the solution in Listing 4 with binary search has more stable run times than the one in Listing 3. 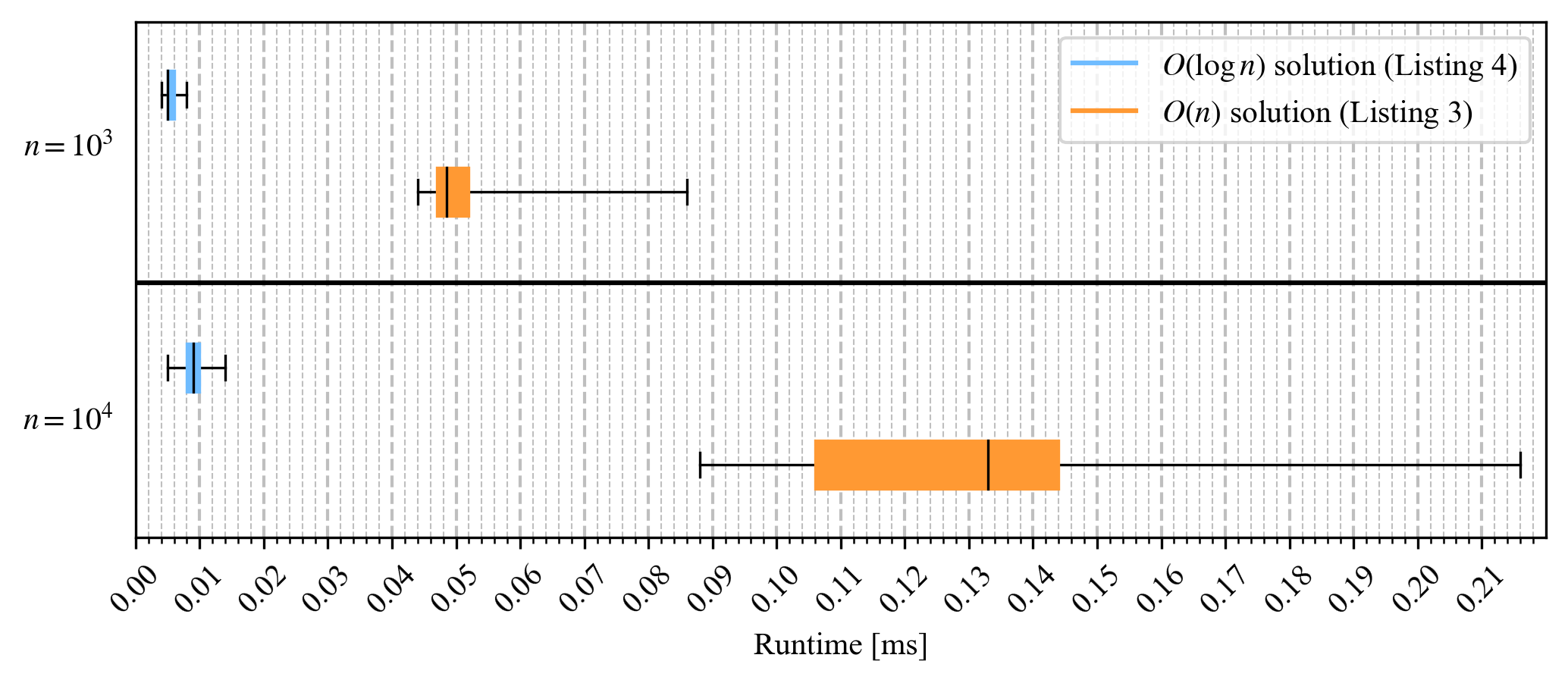Fig. 5: Running times of the respective solution in Task 2

Task 3: Find the largest value in an unsorted list

Now the task is finding the largest value in an unsorted list consisting of integers. One possible solution using the Stream API is to use IntStream and its terminal operation max [8] (Listing 5).

Listing 5

// input
List<Integer> list = List.of(23, 18, 15, 38, 8, 24);

// solution
OptionalInt answer = list.stream().mapToInt(Integer::intValue).max();

This solution has time complexity O(n) and space complexity O(1). A different idea is to sort the list in descending order and return the first value in the list (Listing 6). As previously mentioned, Java provides several ways of sorting a list. To sort in descending order, you must specify a comparator in Java that compares backwards, since by default, the list is sorted in ascending order. You must also not use an immutable list, except when working with the intermediate sorted operation in the Stream API, because the sort methods will process the list directly. For instance, the List.of method returns an immutable list.

Listing 6

// input
List<Integer> list = Arrays.asList(23, 18, 15, 38, 8, 24);

// solution
list.sort(Collections.reverseOrder()); int answer = list.get(0);

This solution has time complexity O(nlogn). However, the solution’s space complexity depends on the method used in the implementation of the sort method. As previously seen in Figure 1, the time complexity O(nlogn) is worse than O(n). In fact, you can see in Figure 6 that as the length of the input list n increases, the solution’s runtime from Listing 6 also increases dramatically with sorting—more than it did in Listing 5. However, in the next task, we will see that in certain cases, sorting the list is a good idea. 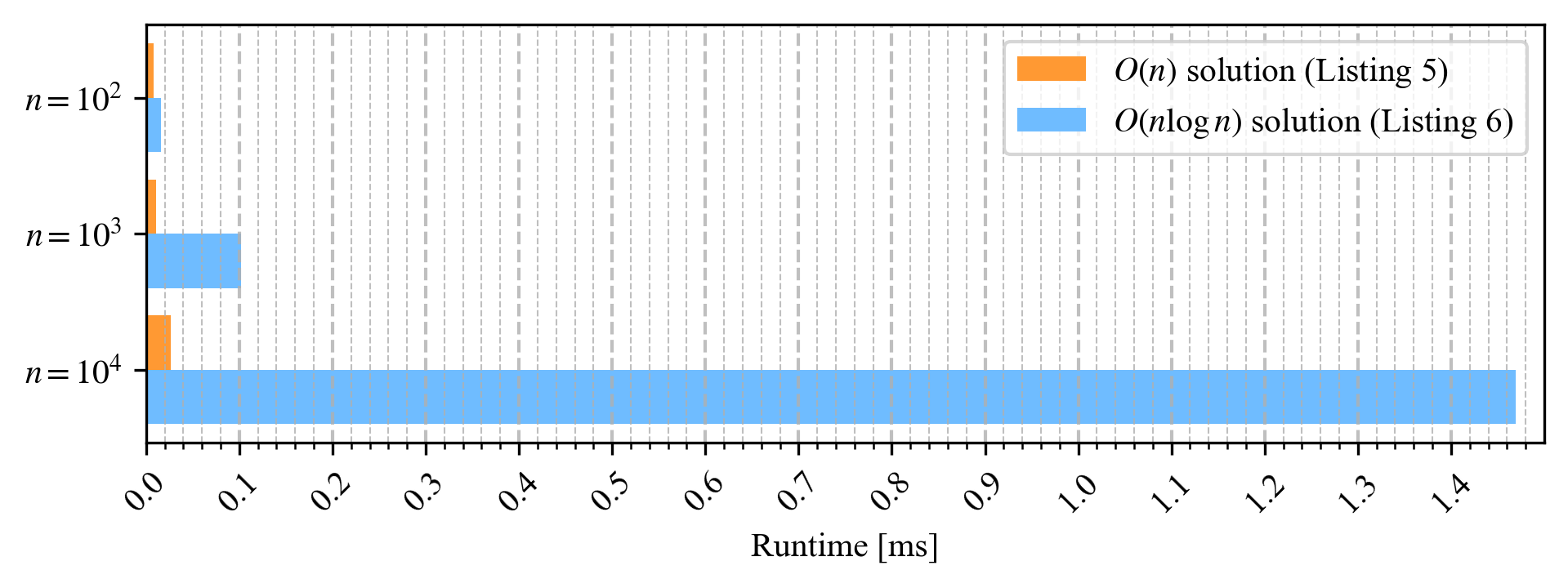Fig. 6: Average runtimes of the respective solution for Task 3

Task 4: Find the largest k elements in an unsorted list

In the last task, we saw that sorting isn’t necessary if you only want to know the largest value of an unsorted list. What about needing the k largest values from the list? So, if k = 3, then you must find the three largest values from the list (assuming that k is less than the input length). In this case, it’s no longer enough to iterate through the input list once. But the solution with sorting will continue to work (Listing 7).

Listing 7

// input
List<Integer> list = Arrays.asList(23, 18, 15, 38, 8, 24);
int k = 3;

// solution
list.sort(Collections.reverseOrder());
List<Integer> answer = list.subList(0, k);

This solution can be easily optimized with a priority queue. A priority queue is implemented in Java with a binary heap [9] and is an abstract data structure that can be used to query the smallest value (or largest, depending on which comparator is specified) in the queue. Generally, the time complexity for adding and deleting values is O(logn). For querying the smallest value, it is O(1), where n is the length of the priority queue. In our case, we add individual elements from the input list to the priority queue and delete each time the smallest value from the priority queue as soon as the queue’s size is greater than k. Lastly, you insert individual elements from the priority queue into a list. Listing 8 shows a sample implementation of this solution. A small optimization, the priority queue is instantiated with an initial capacity of k+1 since it can contain k+1 elements at most. This solution’s time complexity is O(nlogk), since you insert n elements from the input list into the priority queue at a time, but the priority queue’s size is limited to k. The space complexity is O(k) because you keep k elements in the priority queue temporarily so that you can eventually create the result list. Figure 7 shows the average run times of the respective solutions when measured with different lengths for input list n. The larger the difference between n and k, the larger its effect on the runtime. 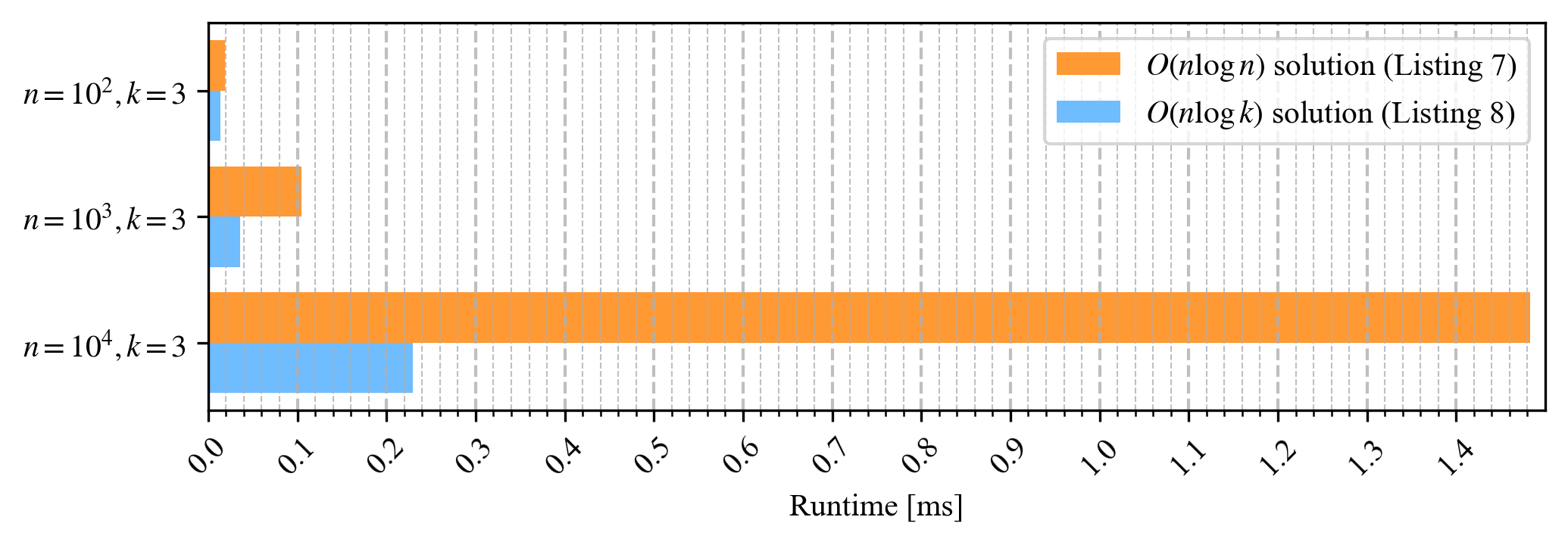Fig. 7: Average runtimes of the corresponding solution for Task 4

Listing 8

// input
List<Integer> list = List.of(23, 18, 15, 38, 8, 24);
int k = 3;

// solution
Queue<Integer> queue = new PriorityQueue<>(k+1);
for(int v : list) {
queue.offer(v);
if(queue.size() > k) {
queue.poll();
  }
}
List<Integer> answer = Stream.generate(queue::poll)
.takeWhile(Objects::nonNull).collect(Collectors.toList());

Conclusion

In this article, I summarized the ideas of time and space complexities, and—in particular—I compared how time complexity affects runtime when working with a large amount of data. It’s good practice to keep the two measures in mind and consider other criteria like code readability or maintainability during trade-offs. The Stream API is a very powerful tool for smaller data sets. But basically, the time complexity is O(n) if you filter or search over the entire input and don’t prematurely terminate. If there’s a possibility of the input growing in the future, then from the beginning you should consider if there’s a better solution from the point of view of both complexities.