Development, training and deployment of neural networks
Because of the features mentioned above, PyTorch is popular above all with deep learning researchers and Natural Language Processing (NLP) developers. Significant innovations were also introduced in the last version, the first official release 1.0, in the area of integration and deployment as well.
Tensors
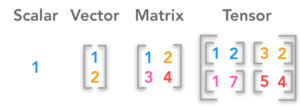
The elementary data structure for representing and processing data in PyTorch is torch.Tensor, The mathematical term tensor stands for a generalization of vectors and matrices. Tensors in the form of multidimensional arrays are implemented in PyTorch. Here a vector is nothing more than a one-dimensional tensor (or a tensor with rank 1) the elements of which can be numbers of a certain data type (such as torch.float64 or torch.int32) could be. A matrix is thus a two-dimensional tensor (rank 2) and a scalar is a zero-dimensional tensor (rank 0). Tensors of even higher dimensions do not have any special names (Fig. 1).
Figure 1: Tensors
The interface for PyTorch tensors strongly relies on the design of multidimensional arrays in NumPy. Like NumPy, PyTorch provides predefined methods which can be used to manipulate tensors and perform linear algebra operations. Some examples are shown in Listing 1.
# Generation of a one-dimensional tensor with # 8 (uninitialized) elements (float32) x = torch.Tensor(8) x.double() # Conversion to float64 tensor x.int() # Conversion to int32 data type # 2D long tensor preinitialized with zeros x = torch.zeros([2, 2]) # 2D long tensor preinitialized with ones # and subsequent conversion to int64 y = torch.ones([2, 3]).long() # Merge two tensors along dimension 1 x = torch.cat([x, y], 1) x.sum() # Sum of all elements x.mean() # Average of all elements # Matrix multiplication x.mm(y) # Transpose x.t() # Inner product of two tensors torch.dot(x, y) # Calculates intrinsic values and vectors torch.eig (x) # Returns tensor with the sine of the elements torch.sin(x)
The use of optimized libraries such as BLAS, LAPACK and MKL allows for high-performance execution of tensor operations on the CPU (especially with Intel processors). In addition, PyTorch (unlike NumPy) also supports the execution of operations on NVIDIA graphic cards using the CUDA toolkit and the CuDNN library. Listing 2 shows an example of how to move tensor objects to the memory of the graphic card to perform optimized tensor operations there.
Listing 2
# 1D Tensors
x = torch.ones(1)
y = torch.zeros(1)
# Move tensors to the GPU memory
x = x.cuda()
y = y.cuda()
# or:
device = torch.device("cuda")
x = x.to(device)
y = y.to(device)
# The addition operation is now performed on the GPU
x + y # like torch.add(x, y)
# Copy back to the CPU
x = x.cpu()
y = y.cpu()
Since NumPy arrays are more or less considered to be standard data structures in the Python data science community, frequent conversion from PyTorch to NumPy and back is necessary in practice. These conversions can be done easily and efficiently (Listing 3) because the same memory area is shared and no copying of memory content is required.
Listing 3 # Conversion to NumPy x = x.numpy() # Conversion back as PyTorch tensor y = torch.from_numpy(x) # y now points to the same memory area as x # a change of y changes x at the same time
Learn more about ML Conference:
Network Modules
The torch.nn library contains many tools and predefined modules for generating neural network architectures. In practice, you define your own networks by deriving the abstract torch.nn.Module class, Listing 4 shows the implementation of a simple feed-forward network with a hidden layer and one tanh activation listed.
Listing 4
import torch
import torch.nn as nn
class Net(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(Net, self).__init__()
# Here you create instances of all submodules of the network
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.act1 = nn.Tanh()
self.fc2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
# Here you define the forward sequence
# torch.autograd dynamically generates a graph on each run
x = self.fc1(x)
x = self.act1(x)
x = self.fc2(x)
return x
In the process, a network class of the abstract .Module class is derived. The __init__() and forward() methods must be defined at the same time. In __init __ (), we need to instantiate and initiate all the required elements that make up the entire network. In our case, we generate three elements:
-
- fc1 – using nn.Linear (input_dim, hidden_dim) we generate a fully connected layer with an input dimension of input_dim and an output dimension of hidden_dim
-
- act1 – a Tanh activation function
- fc2 – another fully connected layer with an input dimension of hidden_dim and an output dimension of output_dim.
The sequence in __init() __ basically does not matter, but for stylistic reasons you should generate them in the order in which they are called in the forward() method. The sequence in the forward() method is decisive for processing – this is where you determine the sequences of the forward run. At this point, you can even build in all kinds of conditional queries and branches, since a calculation graph is dynamically generated on each run (Listing 5). This is useful if for example you want to work with varying batch sizes or experiment with complex branches. In particular, the processing of sequences of different lengths as input – as is often the case with many NLP problems – is much easier to realize with dynamic graphs than with static ones.
Listing 5
class Net(nn.Module):
...
def forward(self, x, a, b):
x = self.fc1(x)
# Conditional application of the activation function
if a > b:
x = self.act1(x)
x = self.fc2(x)
return x
“Autograd” and dynamic graphs
PyTorch uses the torch.autograd package to dynamically generate a directed acyclic graph (DAG) on each forward run. In contrast, in the case of static generation, the graph is completely constructed initially and is then no longer changed. The static graph is filled and executed at each iteration with the new data. Dynamic graphs have some advantages in terms of flexibility, as I had already explained in the previous section. The disadvantages concern optimization capabilities, distributed (parallel) training and deployment of the models.
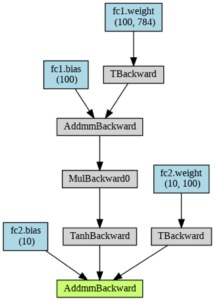
Through the definition of the forward path, torch.autograd generates a graph; the nodes of the graph represent the tensors and the edges represent the elementary tensor operations. With the help of this information, the gradients of all tensors can be determined automatically at runtime and thus back propagation can be carried out efficiently. An example graph is shown in Figure 2.
Figure 2: Example of a DAG generated using “torch.autograd”
Debugger
The biggest advantage in the implementation of dynamic graphs rather than static graphs is the possibility of debugging. Within the forward () method, you can make any printout or set breakpoints, which in turn can be analyzed, for example with the help of the pdb standard debugger. This feature is not readily available with static graphs, because you do not have direct access to the objects of the network at runtime.
Training
The torchvision package contains many useful tools, pre-trained models and datasets for image processing. In Listing 6, the FashionMNIST dataset is loaded. It consists of a training and validation dataset containing 60,000 or 10,000 icons from the fashion industry.
Listing 6
transform = transforms.Compose([transforms.ToTensor()])
# more examples of transformations:
# transforms.RandomSizedCrop()
# transforms.RandomHorizontalFlip()
# transforms.Normalize()
# Download and load the training data set (60,000)
trainset = datasets.FashionMNIST('./FashionMNIST/', download=True, train=True, transform=transform) # Object from torch.utils.data.class dataset
trainloader = DataLoader(trainset, batch_size=batch_size, shuffle=True, num_workers=4)
# Download and load the validation dataset (10,000)
validset = datasets.FashionMNIST('./FashionMNIST/', download=True, train=False, transform=transform) # Object from torch.utils.data.class dataset
validloader = DataLoader(validset, batch_size=batch_size, shuffle=True, num_workers=4)
Figure 3: Examples from the “FashionMNIST” dataset
The icons are grayscale images of 28×28 pixels divided into ten classes (0-9): 0. T-Shirt, 1. Trousers, 2. Sweater, 3. Dress, 4. Coat, 5. Sandals, 6. Shirt, 7. Sneakers, 8. Bag, 9. Ankle Boot (Fig. 3). The dataset class represents a dataset that can be partitioned arbitrarily and applied to various transformations. In this example, the NumPy arrays are converted to Torch tensors. In addition though, quite a few other transformations are offered to augment and normalize the data (such as snippets, rotations, reflections, etc.). Data Loader is an iterator class that generates individual batches of the dataset and loads them into memory, so you do not have to completely load large data sets. Optionally, you can choose whether you want to start multiple threads (num_workers) or whether the dataset should be remixed before each epoch (shuffle).
In Listing 7, we first generate an instance of our model and transfer the entire graph to the GPU. PyTorch offers various loss functions and optimization algorithms. For a multi-label classification problem, CrossEntropyLoss () can be for example chosen as a loss function, and Stochastic Gradient Descent (SGD) as the optimization algorithm. The parameters of the network that should be optimized are transferred to the SGD() method. An optional parameter is the learning rate (lr).
Listing 7
import torch.optim as optim
# Use the GPU if available
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Define model
input_dim = 784
hidden_dim = 100
output_dim = 10
model = Net(input_dim, hidden_dim, output_dim)
model.to(device) # move all elements of the graph to the current device
# Define optimizer algorithm and associate with model parameters
optimizer = optim.SGD(model.parameters(), lr=0.01)
# Define loss function: CrossEntropy for classification
loss_function = nn.CrossEntropyLoss()
The train() function in Listing 8 performs a training iteration. At the beginning, all gradients of the network graph are reset (zero_grad()). A forward run through the graph is performed afterwards. The loss value is determined by comparing the network output and the label tensor. The gradients are calculated using backward() and finally, the weights of the network are updated through back propagation using optimizer.step(). The valid() validation iteration is a variant of the training iteration, and all back propagation work steps are omitted in the process.
Listing 8
# Training a batch
def train(model, images, label, train=True):
if train:
model.zero_grad() # Reset the gradients
x_out = model(images)
loss = loss_function(x_out, label) # Determine loss value
if train:
loss.backward() # Calculate all gradients
optimizer.step() # Update the weights
return loss
# Validation: Only forward run without back propagation
def valid(model, images, label):
return train(model, images, label, train=False)
The full iteration over multiple epochs is shown in Listing 9. For the application of the Net() feed forward model, the icon tensors with the dimensions (batch_size, 1, 28, 28) must be transformed to (batch_size, 784). The call of train_loop() should thus be executed with the ‘flatten’ argument:
train_loop(model, trainloader, validloader, 10, 200, ‘flatten’).
Listing 9
import numpy as np
def train_loop(model, trainloader, validloader=None, num_epochs = 20, print_every = 200, input_mode='flatten', save_checkpoints=False):
for epoch in range(num_epochs):
# Training loop
train_losses = []
for i, (images, labels) in enumerate(trainloader):
images = images.to(device)
if input_mode == 'flatten':
images = images.view(images.size(0), -1) # flattening of the Image
elif input_mode == 'sequence':
images = images.view(images.size(0), 28, 28) # Sequence of 28 elements with 28 features
labels = labels.to(device)
loss = train(model, images, labels)
train_losses.append(loss.item())
if (i+1) % print_every == 0:
print('Training', epoch+1, i+1, loss.item())
if validloader is None:
continue
# Validation loop
val_losses = []
for i, (images, labels) in enumerate(validloader):
images = images.to(device)
if input_mode == 'flatten':
images = images.view(images.size(0), -1) # flattening of the Image
elif input_mode == 'sequence':
images = images.view(images.size(0), 28, 28) # Sequence of 28 elements with 28 features
labels = labels.to(device)
loss = valid(model, images, labels)
val_losses.append(loss.item())
if (i+1) % print_every == 0:
print('Validation', epoch+1, i+1, loss.item())
print('--- Epoch, Train-Loss, Valid-Loss:', epoch, np.mean(train_losses), np.mean(val_losses))
if save_checkpoints:
model_filename = 'checkpoint_ep'+str(epoch+1)+'.pth'
torch.save({
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
}, model_filename)
Save and load trained weights
To be able to use the models later for inference in an application, it is possible to save the trained weights in the form of serialized Python Dictionary objects. The Python package pickle is used for this. If you want to continue training the model later, you should also save the last state of the optimizer. Listing 9 stores the model weights and current state of the optimizer after each epoch. Listing 0 shows how one of these pickle files can be loaded.
Listing 10
model = Net(input_dim, hidden_dim, output_dim)
checkpoint = torch.load('checkpoint_ep2.pth')
model.load_state_dict(checkpoint['model_state_dict'])
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
Network Modules
PyTorch offers many more predefined modules for building Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), or even more complex architectures such as encoder-decoder systems. The Net() model could for example be extended with a dropout layer (Listing 11).
Listing 11
class Net(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(Net, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.dropout = nn.Dropout(0.5) # Dropout layer with probability 50 percent
self.act1 = nn.Tanh()
self.fc2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
x = self.fc1(x)
x = self.dropout(x) # Dropout after the first FC layer
x = self.act1(x)
x = self.fc2(x)
return x
Listing 12 shows an example of a CNN consisting of two Convolutional Layers with Batch Normalization, each with ReLU activation and a Max Pooling Layer. The training call could look like this:
model = CNN(10).to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01)
train_loop(model, trainloader, validloader, 10, 200, None)
Listing 12
class CNN(nn.Module):
def __init__(self, num_classes=10):
super(CNN, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 16, kernel_size=5, padding=2),
nn.ReLU(),
nn.MaxPool2d(2)
)
self.layer2 = nn.Sequential(
nn.Conv2d(16, 32, kernel_size=5, padding=2),
nn.ReLU(),
nn.MaxPool2d(2))
self.fc = nn.Linear(7*7*32, 10)
def forward(self, x):
out = self.layer1(x)
out = self.layer2(out)
out = out.view(out.size(0), -1) # Flattening for FC input
out = self.fc(out)
return out
</code>
An example of an LSTM network which has been optimized using the Adam Optimizer is shown in Listing 13. The pixels of the images from the <em>FashionMNIST</em> dataset are interpreted as sequences of 28 elements, each with 28 features and preprocessed accordingly.
[code title="Listing 13"]
Listing 13
# Recurrent Neural Network
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers, num_classes):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, num_classes)
def forward(self, x):
# Initialize Hidden and Cell States
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
out, _ = self.lstm(x, (h0, c0))
out = self.fc(out[:, -1, :]) # last hidden state
return out
sequence_length = 28
input_size = 28
hidden_size = 128
num_layers = 1
model = LSTM(input_size, hidden_size, num_layers, output_dim).to(device)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
train_loop(model, trainloader, validloader, 10, 200, 'sequence')
</code>
The torchvision package also allows you to load known architectures or even pre-trained models that you can use as a basis for your own applications or for transfer learning. For example, a pre-trained VGG model with 19 layers can be loaded as follows:
<ol>from torchvision import models</ol>
<ol>vgg = models.vgg19(pretrained=True)</ol>
<h2><strong>Deployment</strong></h2>
The integration of PyTorch models into applications has always been a challenge, as the opportunities to use the trained models in production systems had been relatively limited. One commonly used method is the development of a REST service, using <a href="http://flask.pocoo.org">flask</a>, for example. This REST service can run locally or within a Docker image in the cloud. The three major providers of cloud services (AWS, GCE, Azure) now also offer predefined configurations with PyTorch.
An alternative is conversion to the <a href="https://onnx.ai">ONNX format</a>. ONNX (Open Neural Network Exchange Format) is an open format for the exchange of neural network models, which are also supported by <a href="https://mxnet.apache.org">MxNet</a> and <a href="https://caffe.berkeleyvision.org">Caffe</a>, for example. These are machine learning frameworks that are used productively by Amazon and Facebook. Listing 14 shows an example of how to export a trained model to the ONNX format.
[code title="Listing"]
Listing 14
model = CNN(output_dim)
# Any input sensor for tracing
dummy_input = torch.randn(1, 1, 28, 28)
# Conversion to ONNX is done by tracing a dummy input
torch.onnx.export(model, dummy_input, "onnx_model_name.onnx")
TorchScript and C++
As of version 1.0, PyTorch has also been offering the possibility to save models in LLVM-IR format. This can be done completely independently of Python. The tool for this is TorchScript, which implements its own JIT compiler and special optimizations (static data types, optimized implementation of tensor operations).
Listing 15
# Any input sensor for tracing
dummy_input = torch.randn(1, 1, 28, 28)
traced_model = torch.jit.trace(model, dummy_input)
traced_model.save('jit_traced_model.pth')
You can create the TorchScript format in two ways. For one, by tracing an existing PyTorch model (Listing 15) or through direct implementation as a script module (Listing 16). In script mode, an optimized static graph is generated. This not only offers the advantages for deployment mentioned earlier, but could, also be used for distributed training, for example.
Listing 16
from torch.jit import trace
class Net_script(torch.jit.ScriptModule):
def __init__(self, input_dim, hidden_dim, output_dim):
super(Net_script, self).__init__()
self.fc1 = trace(nn.Linear(input_dim, hidden_dim), torch.randn(1, 784))
self.fc2 = trace(nn.Linear(hidden_dim, output_dim), torch.randn(1, 100))
@torch.jit.script_method
def forward(self, x):
x = self.fc1(x)
x = torch.tanh(x)
x = self.fc2(x)
return x
model = Net_script(input_dim, hidden_dim, output_dim)
model.save('jit_model.pth')
The TorchScript model can now be integrated into any C ++ application using the C ++ front-end library (LibTorch). This enables high-performance execution of the inference independent of Python and in many different production environments, such as on mobile devices.
Conclusion
With PyTorch, you can efficiently and elegantly develop and train both simple and very complex neural networks. By implementing dynamic graphs, you can experiment with very flexible architectures and use standard debugging tools with no problem. The seamless connection to Python allows for speedy development of prototypes. These features currently make PyTorch the most popular framework for researchers and experiment-happy developers. The latest version also provides the ability to integrate PyTorch models into C ++ applications to achieve better integration in production systems. This is significant progress when compared to the earlier versions. However, other frameworks, especially TensorFlow still have a clear lead in this category. With TF Extended (TFX), TF Serving, and TF Lite, the Google framework provides much more application-friendly and robust tools for creating production-ready models. It will be interesting to see what new developments in this area we will see from PyTorch.
Get to know the ML Conference better?
Here are more sessions
→ Honey Bee Conservation using Deep Learning
→ The Development of (Deep) Reinforcement Learning
→ Understanding how neural networks work by looking at the low level API of TensorFlow 2
→ AI Is Eating Software – How Second Generation AutoML Will Replace Software Development